أجرت LeonaHenryson تحقيقًا عن ما لا يعرفه المصممين من تأثير للرياضيات في مجال عملهم إذا كنت تسأل مصمم ما إذا كان هو أو هي يعتبر نفسه أو تعتبر نفسها موهوبة بشكل خاص في الرياضيات، على الأرجح فإن الجواب سيكون ، لا. ويرجع ذلك إلى أن العديد من الناس الذين يسعون إلى المجالات الفنية يعتقدون أن المهارات المطلوبة للفن و التصميم ببساطة ليس لها علاقة بالمهارات المطلوبة للمهام الرياضياتية كثير من هؤلاء الأفراد لايدركون أن الرياضيات هي جزء لا يتجزأ من التصميم. في الواقع، مفاهيم مثل الأنماط، التماثل، الفضاء، الإيجابية والسلبية، الترتيب، والتسلسل هي في غاية الأهمية للتصميم وكلها لها أساس في الرياضيات.
الُكسيريات (فركتلات) :
الكسيريات وتكرار ألأنماط الهندسية التي تتجمع لتشكل ككل.في الطبيعة كسيريات تشكل الأوراق، الثلج، والهياكل الجيولوجية، وبلورات الجليد. يمكنك حتى فتح برتقالة لرؤية شكل متكرر من اللب مملوء السوائل.هذه هي أيضا كسيريات.
الخلايا البشرية عند فحصها تحت المجهر مصنوعة أيضا من تكرار كسيريات صغيرة.يمكن للعلماء استخدام الحواسيب والصيغ الرياضياتية لخلق نماذج من أي شيء تقريبا على أساس الكسيريات ، كلما تحتاج إلى معرفته هو شكل كسيرية في أصغر مستوى ومن ثم الحصول على كسيرية مضاعفة.
المصممين يستخدمون الكسيريات في كل شيء من تصميم الملابس لخلفيات الموقع. و التعرجات هي مثال على الطرق التي يمكن من خلالها للكسيريات أن تصل إلى التصميم. وفيما يلي مثال على الكسيريات المستخدمة لأغراض التصميم .
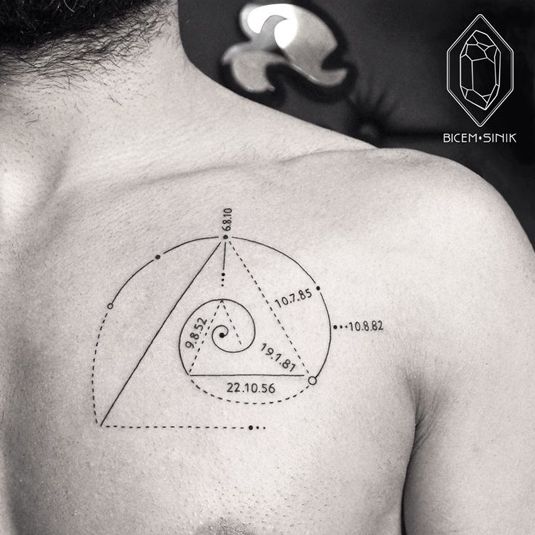
متتالية فيبوناتشي :
دعونا لعب لعبة سريعة. نلقي نظرة على التسلسل التالي من الأرقام ومحاولة تحديد أي عدد سيأتي بعدها؟ ...55،34،21،13،8،5،3،2،1،1،0 فكر جيدًا...!
إذا كنت تفكر في89،جوابك صحيح تماما.النمط في هذه الأرقام هو تسلسل فيبوناتشي. نلقي نظرة على الأرقام مرة أخرى. كل رقم هو مجموع الرقمين اللذين يسبقانه. تسلسل فيبوناتشي، تحتاج فقط إلى متسلسلة مع عدد بداية ثم مضاعفة هذا العدد لبدء النمط.
إذا كنت تفكر في89،جوابك صحيح تماما.النمط في هذه الأرقام هو تسلسل فيبوناتشي. نلقي نظرة على الأرقام مرة أخرى. كل رقم هو مجموع الرقمين اللذين يسبقانه. تسلسل فيبوناتشي، تحتاج فقط إلى متسلسلة مع عدد بداية ثم مضاعفة هذا العدد لبدء النمط.

قد تتسائل في هذه المرحلة ما علاقة كل من هذا مع الفن. عندما يتم ترجمة هذه الأرقام إلى أشكال أنماط مختلفة تظهر بما في ذلك اللوالب، الأزهار، والتفرعات. ويمكن رؤية هذه الأشكال في الطبيعة وفي الفن.
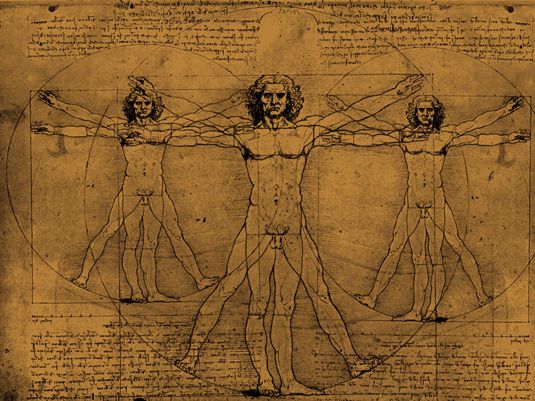
اللوالب، كما تعلمون تظهر كثيرا في التصميم. مرتبة بطرق أخرى، أرقام فيبوناتشيت شكل أساس النجوم و العديد من الأشكال الهندسية الأخرى . حتى الوجه. الإنساني يتبع عن كثب هذا النمط. .
الهندسة المعمارية التاريخية مثل الأهرامات و البارثينون تحتوي أيضا على تسلسل فيبوناتشي إذا قمت بفحصها عن كثب. لمعرفة المزيد عن الطرق التي أثرت على هذا النمط من الأرقام في الفن، يمكنك القيام ببعض البحوث على اعمال دافنشي .وهو معروف جدا بإدراجه النسبة الذهبية لفيبوناتشي في عمله .
المصدر :
ترجمة : ضرغام لبنان
تدقيق : نبأ عبد الأمير
تدقيق : نبأ عبد الأمير