كيف قادنا مربع صغير إلى مفهوم اللانهاية؟ — من فيثاغورس إلى رامانوجان
هل تساءلت يومًا كيف يمكن لمربع صغير أن يغيّر مجرى التاريخ الرياضي؟
في هذه التدوينة، ننطلق من نظرية فيثاغورس التي عرفناها جميعًا في المدرسة، لنكتشف كيف قادت إلى أعداد لا تنتهي، ومفاهيم أذهلت أعظم العقول مثل رامانوجان.
رحلة ممتعة تبدأ بسؤال بسيط… وتنتهي عند حدود اللانهاية!
a² + b² = c²
حوالي سنة 500 قبل الميلاد، أصبح واحدًا من عمالقة الفكر الرياضي في التاريخ. لكن، وكما تُظهر لنا مسيرة العلم مرارًا وتكرارًا، فإن كل اكتشاف عظيم لا يقدّم إجابة فقط… بل يفتح أبوابًا لأسئلة جديدة، ويوجه التفكير نحو آفاق أعمق، ويهيئ الطريق لاكتشافات قادمة.
فهم نظرية فيثاغورس
تنص نظرية فيثاغورس على أن:
مساحة المربع المنشأ على الوتر (أي الضلع المقابل للزاوية القائمة في مثلث قائم الزاوية) تساوي مجموع مساحتي المربعين المنشأين على الضلعين الآخرين.
بعبارة أخرى، إذا كان لدينا مثلث قائم الزاوية أطوال ضلعيه القائمين هما a و b، فإن طول الوتر c يخضع للعلاقة:
a² + b² = c²
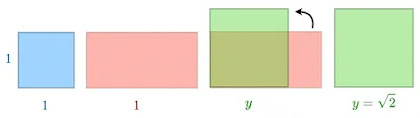
السؤال الغامض: ما طول ضلع المربع الذي مساحته ضعف مربع طوله 1؟
فلنفكك هذا السؤال:
- إذا كان لدينا مربع طوله 1، فمساحته = 1 × 1 = 1
- نريد الآن مربعًا آخر مساحته = 2
- فما هو طول ضلع هذا المربع الجديد؟ لنفترض أن طوله هو y، إذن:
y² = 2 ⇒ y = √2
وهنا كانت الصدمة الفكرية: الجذر التربيعي لـ 2 لا يمكن كتابته على صورة كسر، أي أنه عدد غير نسبي! وهذا الاكتشاف هزّ الفكر الإغريقي الذي كان يؤمن بأن كل شيء يمكن التعبير عنه بالنسب (الكسور).
من فيثاغورس إلى اللانهاية
هذا النوع من التساؤلات لم يتوقف، بل امتد ليصل إلى علماء كبار مثل سيرينفاسا رامانوجان، الذي استكشف عالم الأعداد اللانهائية والجذور والسلاسل الرياضية العجيبة.
لقد كشف هذا السؤال البسيط عن حدود الفهم الرياضي القديم، وفتح بابًا لفهم أوسع لمفهوم العدد، سواء أكان نسبيًا أم غير نسبي، منتهيًا أم غير منتهٍ.
خاتمة
ما يبدو تمرينًا بسيطًا في الرياضيات قد يكون بداية ثورة فكرية. من نظرية فيثاغورس البسيطة إلى تساؤل عن √2، ثم إلى مفاهيم مثل الأعداد غير النسبية واللانهاية، كل ذلك بدأ من مربع بطول 1!
في التدوينات القادمة، سنكشف كيف تطورت هذه الأسئلة إلى مفاهيم عظيمة في الرياضيات مثل الأعداد الحقيقية، والهندسة التحليلية، والنظرية الحديثة للأعداد.
تابعنا في رحلة تبسيط الرياضيات واكتشاف أسرارها من أقدم النظريات إلى أعقد المفاهيم.
المصدر : انقر هنا